The Big Idea: An ETF that buys lottery tickets

Are lottery tickets the ultimate alternative asset?

In 2023, a syndicate out of Malta realized that the Texas Lottery’s jackpot had ticked higher than the cost of buying every ticket¹. The group raised $26M and duly bought virtually every ticket combination, guaranteeing the $95M jackpot. Really clever, although Texas officials don't seem very happy about it.

This was probably against the spirit of the game. That said, buying tickets to improve your odds is the whole point — the scale is what was unusual. So what if the chance to buy millions of tickets was available to anyone? Introducing: $LUCKY, the ETF that buys lottery tickets.

How would it work?

An ETF, broadly, lets you collect a pool of money and invest based on some rules. It might buy the S&P500, or the biggest companies in Italy.

$LUCKY takes a pool of money (the assets under management, or AUM) and puts it all into short term treasury bonds. When the Powerball hits a threshold — call it $584m, the cost of buying every combination — $LUCKY spends 10% of its assets on lottery tickets. If it loses, it waits for the next jackpot. If it wins, $LUCKY holders get paid. Finally, you can get lottery exposure in your IRA.

The odds of winning the Powerball jackpot are 1 in 292,201,338; buying 100 tickets to get to 1 in 2,922,013 doesn’t really change the math. The scale of an ETF could actually change this. 5 million tickets ($10M) is enough to get a 1.71% chance of winning the jackpot. 146 million tickets ($292M) gets you to a 50/50 chance of winning.

Of course, reaching scale requires an absolutely insane amount of money — using our 10% rule, we get a 100% chance of winning the Powerball at $5.8b in AUM. That’s a lot, but there’s at least 300 ETFs bigger than that. Can we make it happen?

The economics of $LUCKY

$LUCKY has one advantage: the allocation to treasuries provides a floor to the real value of the asset. It should track the price of a standard bond ETF… until the Powerball hits the cutoff.

Suddenly, this becomes an extremely risky asset — 10% of the AUM is going into one of the riskiest products out there. At $100m AUM, there’s a 98.3% chance that you’ll lose 10% of the underlying value — a pretty lopsided bet.

So scale really matters. Reaching $500M AUM, $1b AUM, and more dramatically improves the risk to reward ratio. Although the expected value per ticket doesn’t change, the risk-adjusted return improves linearly. As you approach buying every ticket, the value of $LUCKY reaches the value of the treasuries + the jackpot - ticket costs.

So the game theory for $LUCKY is that at low valuations, it’s a treasury. At medium valuations, it’s a treasury with an extremely lopsided bet. And at high valuations, it’s a treasury with a guaranteed additional payout. So how do we get from low to high valuation?

A meme coin model of scalability

The financial instrument of 2024 was the memecoin. A creator ideates a fun gimmick — fartcoin, dogecoin, etc. — and starts building hype. The price skyrockets until it (usually) crashes to roughly $0. You could charitably say that the coins are a way to monetize attention; uncharitably, you could say they try to get a bunch of gamblers to buy $PONZICOIN right before the early adopters cash out.

The problem with memecoins is that there is no model of value beyond attention. Traditional investments, generally, are valued by taking the present value of future cashflows. The cashflows for a memecoin only exist in the imagination of the person who just saw the price crash right after buying in.

But $LUCKY may be the most memeable ETF of all time! You’re buying an interest in a huge amount of lottery tickets, and the odds of winning go up as more people buy in. And for once, there’s actual cashflows — it can’t just randomly collapse to zero.

Memecoins reward people who got in early; imagine the FOMO of missing the chance to (indirectly) actually win the lottery. The memetic value becomes extremely powerful; can we hit the $5.8b in AUM that triggers a guaranteed win? Post aggressively to find out!

So how would this really behave?

Typically, an ETF should trade at Net Asset Value (NAV) — essentially the value of all of the underlying assets the ETF owns. If they own $100m in tech stocks, the total value of the ETF shares should equal the value of the underlying shares: $100m.

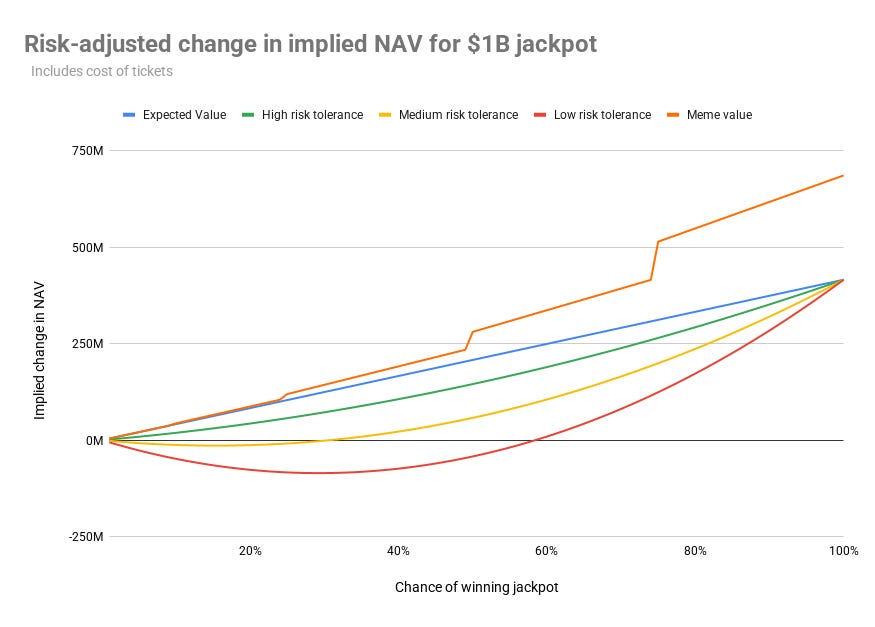
$LUCKY’s implied NAV would be a little different. At a 1% chance of winning, the risk to reward is too lopsided for institutional investors — they’ll want to sell at a discount. But for the right investor, buying low to get disproportionate upside might be really appealing. As money enters the ETF and the odds approach 100%, risk averse money could come back to claim the guaranteed jackpot.

There’s also another possibility — $LUCKY turns into the greatest meme of all time. As it crosses thresholds — 50% chance to win, 75% chance to win — more money flows in completely independent of the real value. Eventually $LUCKY trades at a multiple of the jackpot, for reasons nobody can really explain or stop.

Different risk tolerances provide different perceptions of the NAV as the chance to win increases

This is what makes $LUCKY irresistible — it’s part treasury bond, part high-stakes gamble, and part memecoin unconnected to anything. It has a little something for everybody, and it constantly shifts between reasons to invest.

So what happens after $LUCKY wins?

When you win the lottery, you actually get offered two choices:

1. An annuity, where you get the total jackpot distributed over ~30 years. Typically, it’s a series of payments with an annual 5% increase.

2. A lump sum, where you get the present value of the jackpot as a single payment — usually it’s around 50% of the listed number

This is an important choice that determines the nature of $LUCKY.

The lump sum builds a true lottery at the cost of the prize value. The expected value of buying the lottery tickets would almost always be negative, but variation might attract risk-seeking actors. You don’t want too many though — 100% of tickets purchased guarantees a negative value. The price of $LUCKY would be parabolic, maxing out when there’s still uncertainty. Alternatively, $LUCKY can up their minimum and only enter lotteries after they hit $1B. This has only happened a dozen or so times in history, so $LUCKY would look more like a regular bond ETF with occasional massive volatility.

If $LUCKY takes the annuity, it becomes something really interesting — a diversified bond portfolio. With a guaranteed 5% increase in payout each year, $LUCKY provides predictable cashflows over a 30 year period — and since the SEC requires that ETFs distribute 90% of their net investment income² to shareholders, the annuity income is guaranteed to investors. $LUCKY.ANNUITY could be a hot choice for a 60/40 retirement portfolio.

Wait, this is dumb. How do you buy 292 million lottery tickets?

Very aggressively.

Let’s take a step back: the Powerball runs through a nonprofit called the Multi-State Lottery Association (MUSL). The MUSL handles the prize pool (~50% of the cost of a ticket), the state takes ~30%-40% in tax revenue, and the rest goes to admin and the retailer. States usually set strict regulations on who gets their machines, and typically disallow any kind of automated purchasing or printing.

So taking a lesson from our Maltese friends, $LUCKY would need to physically print these tickets off of machines. A share of $LUCKY’s assets would presumably fund a subsidiary that manages this process.

How many machines would they need? Let's do the math:

• There are 169,200 seconds between drawings

• At 1 ticket printed per second, it would require 1,727 machines running 24 hours a day to print every combination

• A terminal is about 2 feet by 2 feet; if we assume we need 4 sqft feet of clearance around each machine, we need about 62,000 feet of warehouse space to print the tickets, not including storage.

Of course, operations go beyond the printing. How do you organize 292 million tickets? You can imagine a highly sophisticated warehouse like Amazon, with computers directing a massive group of employees which numbers to punch in. With 24 hour a day shifts and robotic automations, the ticket subsidiary may end up as the most extreme example of operational alpha ever.

That said, the Maltese scheme was working with a single-digit number of machines. Getting this many would be an insane task — a standard state lottery might let you get a machine or two, but 1,727 will require some policy entrepreneurship with state officials.

Speaking of: will lotteries love or hate this?

The first reaction to this is, of course lotteries will hate this! They want people to feel like they have a chance of winning; if $LUCKY wins every Powerball, it’s going to really damage the image of the lottery.

But…it also means that there’s nine figures of tickets being bought every single large lottery. It would certainly get a lot of attention, and that attention might let the lottery sellers expand their market — or funnel individuals into new, smaller games. Of course, if $LUCKY starts buying a majority of lottery tickets then there’s no real new value coming in — just money being recycled around.

There’s a bit of game theory here — states usually keep 30% or more of the cost of a Powerball ticket. There’s probably an incentive for a low-tax state to partner with $LUCKY, give them thousands of machines, and collect their share of the millions of tickets. It’s a great deal until they’re kicked out of the Powerball syndicate.

And then there’s everything else

One of the key flaws in this idea is the jackpot is split if two or more people win. This adds insane volatility to the expected outcome; with more players, the chances of a split jackpot go up. This completely uncorrelated risk would be extremely hard to price — although given how many tickets $LUCKY is buying, they may be funding the split jackpot themselves.

Competitor dynamics are a huge risk as well. Once you’re able to buy 100% of the tickets, it’s very hard to enter the market — a new entrant splits the jackpot, causing both funds to lose money. But in the growth stage, it’s possible that a competitor could enter ($CHANCE?). With two players, it would be a race to see who can white knuckle their way through split prizes long enough for the other fund to give up. Unfortunately, there’s only room for one $LUCKY in this market.

Also: ETFs are approved by the SEC. ETFs are required to invest in securities, determined by the Howey Test. The SEC has historically gone after crypto ETFs for not meeting this requirement and I think the lottery idea is, if anything, less defensible. That said, the first Bitcoin Spot ETFs were approved last year; maybe in a lower regulation environment it’s possible? If you’re a securities lawyer reading this, let me know your professional opinion.

Of course, the SEC isn’t the only blocker. Lotteries have state level regulations that are presumably designed to stop this. $LUCKY probably violates the letter and spirit of the contracts signed to purchase a lottery machine, and if it’s not explicitly banned now it probably would be soon.

Official idea rating

1/5 for practicality, 6/5 for fun. This is a cool idea; both the annuity and jackpot models create a truly unique financial instrument. As an annuity, $LUCKY has guaranteed income with low default risk. Stacking enough wins actually has some diversified value as a sort of structured annuity stream.

There’s also a lot of appeal to taking the lump sum. Digital products might be a fun area to explore — offer NFTs to winners of the jackpot, even if they only received 0.0001% of it. Or even more interesting — at low AUM, this is a uniquely uncorrelated way to add volatility and risk to a portfolio. An options market on $LUCKY could be the ultimate pure diversification trade.

While Powerball probably won’t endorse it, I think there’s something to the idea of structured investments in lotteries. But for now, this is probably the domain of private equity companies finding mispricings in small international lotteries. If there’s a firm out there doing lottery arbitrage, please let me know — I want to talk to them.

---

1. For non-lottoheads – most lotteries increase the jackpot every week that it isn’t won. This has the effect of drawing in more players as the jackpot number goes up; sometimes, the jackpot gets high enough to offer a positive expected value (but usually people don’t have the means to buy millions of tickets)

2. Will the SEC count lottery tickets as investment income? A better lawyer than me will have to make that case (I am not a lawyer)